funciones escalonadas

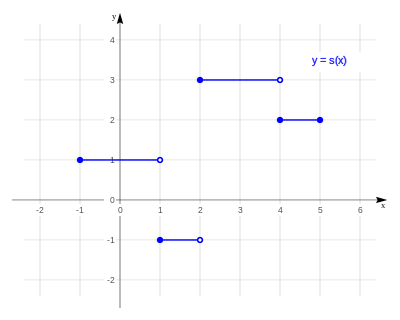
Una función escalonada es aquella función definida a trozos que en cualquier intervalo finito [a, b] en que esté definida tiene un número finito de discontinuidades c₁ < c₂ < ... < c_n, y en cada intervalo ]c_k, c_k+1[ es constante, teniendo discontinuidades de salto en los puntos

Denominamos como (Funciones escalonadas) a aquellas funciones que son definidas en un intervalo [a,b] finito de tal manera que sí mismas se encuentran definidas por medio de trozos (Segmentos), los cuales generán en un cierto sentido discontinuidades en la manera en la cual el comportamiento gráfico de una función se va dando.

Se representan como:

Como su nombre lo dice, su comportamiento gráfico genera la noción como si hubiera unos escalones proyectos es un plano (XY). Donde tales no necesariamente pueden tener un aspecto creciente, pueden tener un aspecto de decrecimiento también.

Dichas son creadas tomando la noción de cada cuando se presento una discontinuidad, lo cual da la posibilidad de definir la longitud de los segmentos a (Trozos).

Dentro de las nociones del analísis matemático existe un herramienta ejemplificada como una función base la cual nos da hincápie a la posibilidad de poder formular una función escalonada con facilidad, debido a que tal se basa en el criterio de una unidad de longitud en lo que respecta a los segmentos (trozos).

Tal es denominada ‘Función escalón unitario o función unitaria de heaviside y es definida como:

os c_k.